最新文章

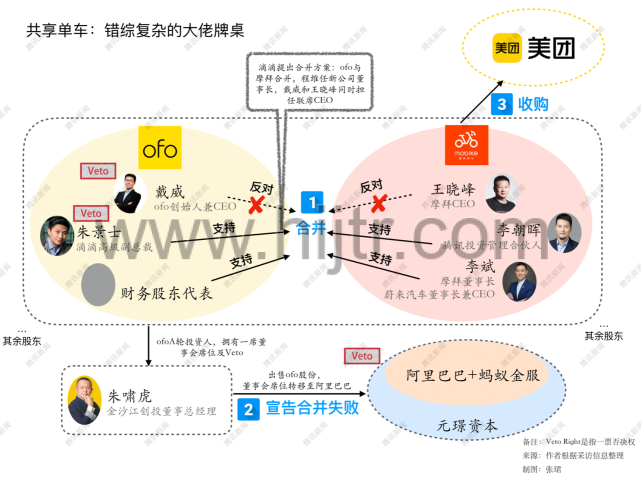
共享单车的智能锁是怎样炼成的？

理论动态 8年前 (2017-10-25) 浏览: 510 评论: 0

在探讨共享单车上智能锁要怎样做出来前，我们应该先弄明白：共享单车是否非要智能锁不可？ 这一切可以从橙黄大战说起。 在如今市场出现的“百车大战”中，OFO 和摩拜无疑是众多市场争夺竞争者中对受瞩目的一对。摩拜单车配备了“GPRS 开锁 + GPS 定位”的智能锁，开发和生产成本较高，而 OFO 走的则是普通自行车密码锁，野蛮铺货大干快跑的策略。 在这场市场占领的竞争中，单纯用机械锁压低单车成本的做法在运营中缺点已经凸显。幻想使用机械锁运营共享单车也在具体的实践中逐渐被证明是不可能的。共享单车上不设

研究进展：汽车共享可能会给城市添堵

理论动态 8年前 (2017-10-24) 浏览: 245 评论: 0

拥堵问题是交通的头号顽疾。解决拥堵问题是很多打车应用的初衷之一。汽车共享被普遍认为对减少道路车辆具有“影响”。但是加州大学戴维斯分校交通运输研究所的一项新研究（虽然还有待更多研究的佐证）认为，这种看法更像是“自我选择偏误”，共享汽车与车辆减少之间并不存在显著的因果关系。该报告给 Uber、Lyft、滴滴等打车应用提出一个质疑：目前情况下，这些 App 给城市带来的究竟是治堵还是添堵？

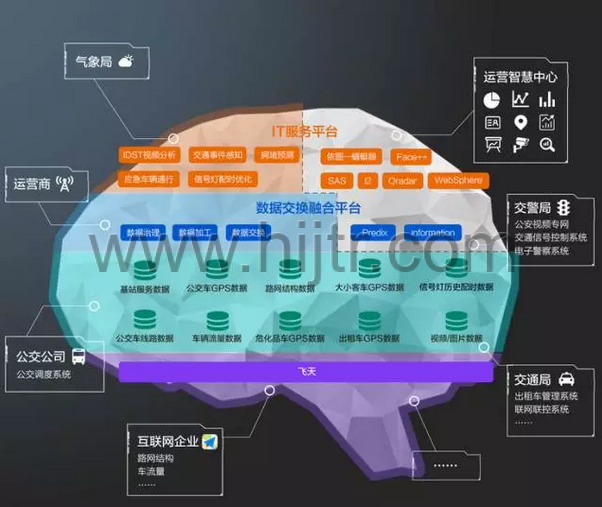
聊聊最近火热的“城市交通大脑”

行业动态 8年前 (2017-10-21) 浏览: 899 评论: 0

窃以为，“城市大脑”的最大贡献在于打通了城市交通数据流转的任督二脉，促进了不同部门不同类型数据的有效融合。对于“城市大脑”，城市管理者给予了极大地期待。虽然从目前来看“城市大脑”建设取得了显著的成就，但随着“城市大脑”接管区域的逐步扩大，其发展将面临巨大的压力。这种压力肯定不是像现在这样单靠增加计算能力就能解决的。

公交改革成败的关键在于城市公共交通的定位

思辨明理 8年前 (2017-10-17) 浏览: 305 评论: 0

公交改革能否成功，关键在于政府对于城市公共交通的定位。很多地方政府嘴里喊着“公交优先”，骨子里还是念着“小汽车优先”。虽然表面上也在大力发展公交，但追求的仅仅是指标的好看，有意无意忽略便民的本质，于是乎公交专用道画在城郊宽阔畅通的马路上这种奇闻屡见不鲜。最后是，口号喊得响，公交服务不见任何改善。

一种神奇的 Sqrt 函数实现方法

模型与算法 8年前 (2017-10-10) 浏览: 2207 评论: 0

在编程开发中，经常需要去计算一个数的平方根，小编一般是直接调用系统函数 Math.Sqrt()。 当然除了系统函数，我们也可以自己编写函数进行求解，常用的方法有二分法和牛顿迭代法。 二分法 二分法的基本思想：对于区间 \([m,n]\) 上连续不断且 \(f(m)·f(n) < 0\) 的函数 \(y=f(x)\)，通过不断地把函数 \(f(x)\) 的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值。 显然，\(\sqrt{a}\) 是函数 \( f(x) =x^

雅虎证实 30 亿用户隐私遭泄露！或涉及几千万中国用户！

热点资讯 8年前 (2017-10-08) 浏览: 294 评论: 0

现如今，网络安全问题层出不穷，用户数据泄露已是屡见不鲜。这要是到了物联网时代，我们将何去何从？

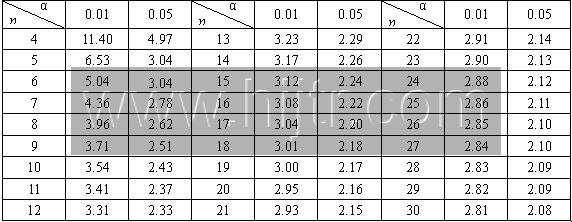
罗曼诺夫斯基检验法（Romanowski）的临界值表

开发随记 8年前 (2017-09-05) 浏览: 1840 评论: 0

罗曼诺夫斯基检验法（Romanowski Test），又称 t 检验，是一种常见的异常数据检测方法，其基本流程为： （1）剔除疑似离群值 \(x_{o}\)，计算新样本的均值和标准差： \[\overline{x'}=\frac{1}{n-1}\sum_{i=1}^{n-1}{x_i} \] \[s'=\sqrt{\frac{1}{n-2}\sum_{i=1}^{n-1}\left({x_i-\overline{x}}\right)^2}\] （2）计算统计量 \(K_{o}\) 的值： \[K

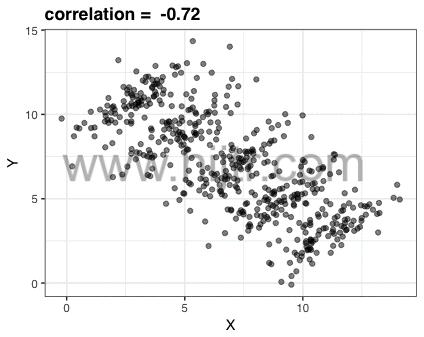
Code for my educational gifs by Rafael Irizarry

热点资讯 8年前 (2017-09-01) 浏览: 496 评论: 0

During preparation for class I sometimes think up of animations that will explain the concept I am teaching. I sometimes share the resulting animations on social media via @rafalab. John Storey recently asked if the source code is publicly available.

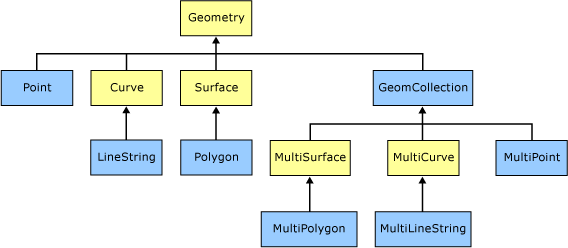
SQL Server 中 Geography 类相关方法的使用

热点资讯 8年前 (2017-08-27) 浏览: 678 评论: 0

--二进制（WKB）表示形式 SELECT geography::STGeomFromText('LINESTRING( -122.360 47.656, -122.343 47.656)', 4326).STAsBinary() --WKT表示形式 SELECT geography::STGeomFromText('LINESTRING(-122.360 47.656, -122.343 47.656)', 4326).STAsText() --空间参考 SELECT geography::S

PHP 常用函数大全

热点资讯 8年前 (2017-08-27) 浏览: 369 评论: 0

字符串相关操作函数 [table id=3 /] 字符串生成与转换 [table id=4 /] 字符串大小写转换 strtolower 将字符串转化为小写 strtoupper 将字符串转化为大写 ucfirst 将字符串的首字母转换为大写 ucwords 将字符串中每个单词的首字母转换为大写 html标签关联 htmlentities 将字符转换为HTML实体 htmlspecialchars 预定义字符串转HTML编码 nl2br 在字符串所有新行之前插入 HTML 换行标记 \n转换为&